Você já deve ter esbarrado em postagens nas redes sociais alardeando um raríssimo alinhamento dos planetas que ocorreria em algum momento de 2025, não? Então esse post é pra você!
Precisamos falar um pouco sobre isso! Mas primeiro vamos esclarecer alguns conceitos astronômicos pra alinhar nossa conversa.
Alinhamento dos Planetas x Conjunção
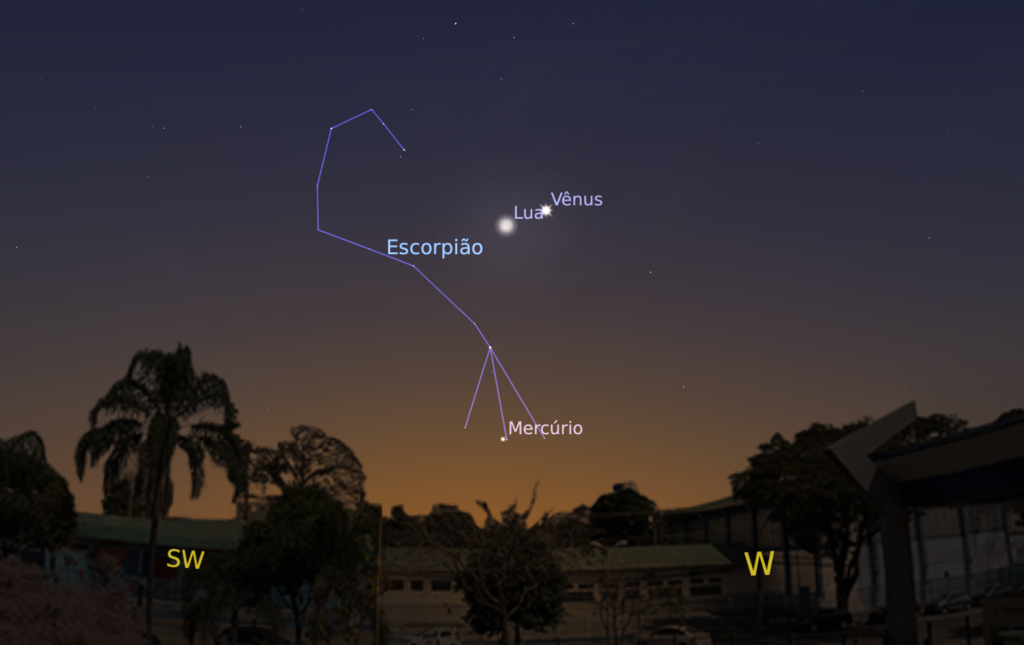
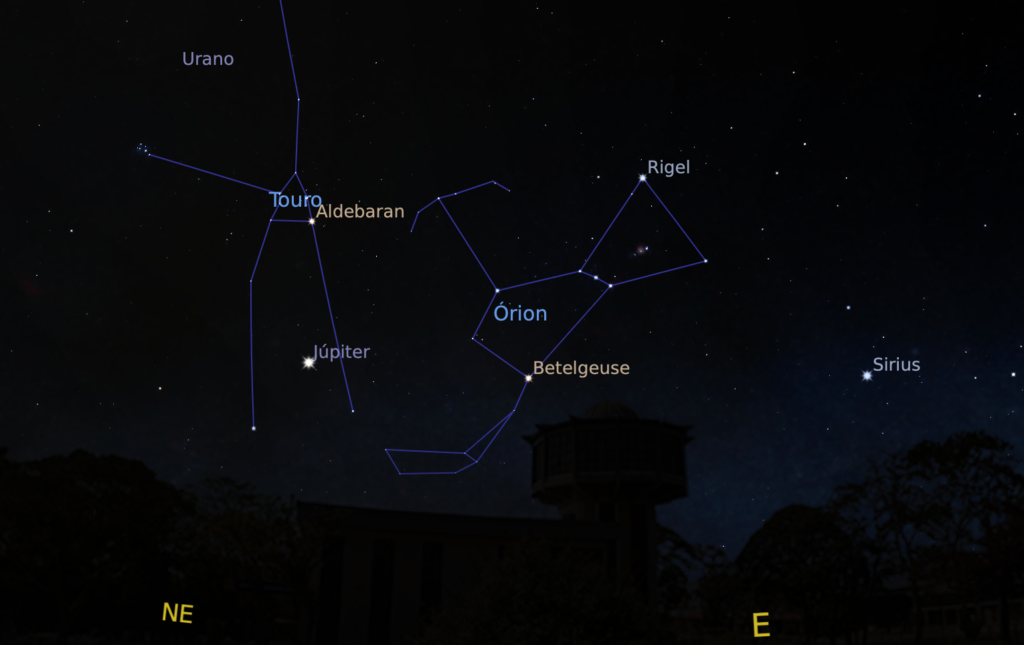
A imagem que abre este post mostra 6 planetas e a Lua simultaneamente na mesma imagem. Saturno também estava visível no céu, mas estava fora do campo da câmera. É fácil notar que todos esses objetos estão aproximadamente sobre a mesma linha. E isso não é uma coincidência!

Todos os planetas orbitam o Sol aproximadamente no mesmo plano, então sempre os veremos próximos da linha que conhecemos como eclíptica. A eclíptica desenha no céu, o plano da órbita terrestre em torno do Sol.
Assim, veremos sempre os planetas alinhados. Formando esse cortejo no céu. No entanto, este alinhamento dos planetas não é uma CONJUNÇÃO.
Então, o que seria uma “Conjunção“?

Quando vemos um objeto do Sistema Solar na mesma direção de outro objeto, que pode ou não ser do Sistema Solar, dizemos que esses objetos estão em conjunção. Ou seja, ambos estão posicionados ao longo de nossa linha de visada. Na imagem acima, vemos uma conjunção entre Vênus e a Lua.
A cada mês, por exemplo, ao orbitar a Terra, a Lua emparelhará com cada um dos planetas e com algumas estrelas brilhantes. Em nosso calendário astronômico mensal, sempre indicamos essas conjunções entre a Lua e planetas e estrelas.
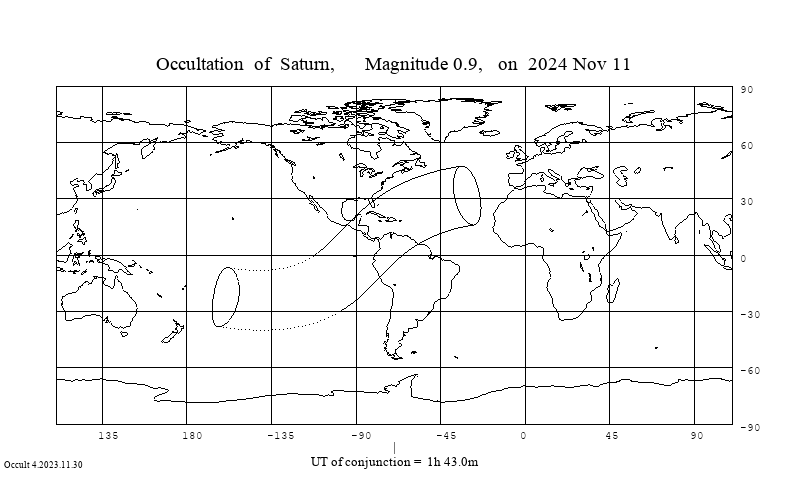
Em geral, não há nada de raro nessas conjunções, que sempre acontecem a cada mês. No entanto, em algumas ocasiões o alinhamento dos planetas com a Lua é tão perfeito que a Lua chega a ocultar o objeto mais distante, como na imagem abaixo, quando a Lua ocultou Marte na madrugada de 6 de setembro de 2020. Em 2020, duas ocultações de Marte foram visíveis de parte do Brasil.

Você agora entendeu o conceito mais importante deste post: numa conjunção, temos um alinhamento dos planetas ou de outros astros ao longo de nossa linha de visada.
Sem alinhamento dos planetas não tem nada legal pra ver no céu?
Tem muita coisa legal pra ver no céu sim! Mas o Universo é um lugar bem grande e sempre tem algo fascinante pra ser observado. Uma conjunção é certamente um belo evento, mas observar os planetas separados também é uma experiência que não dispensamos! No início de Janeiro poderemos ver a Lua pouco depois da fase nova emparelhando com Vênus e Saturno no céu.
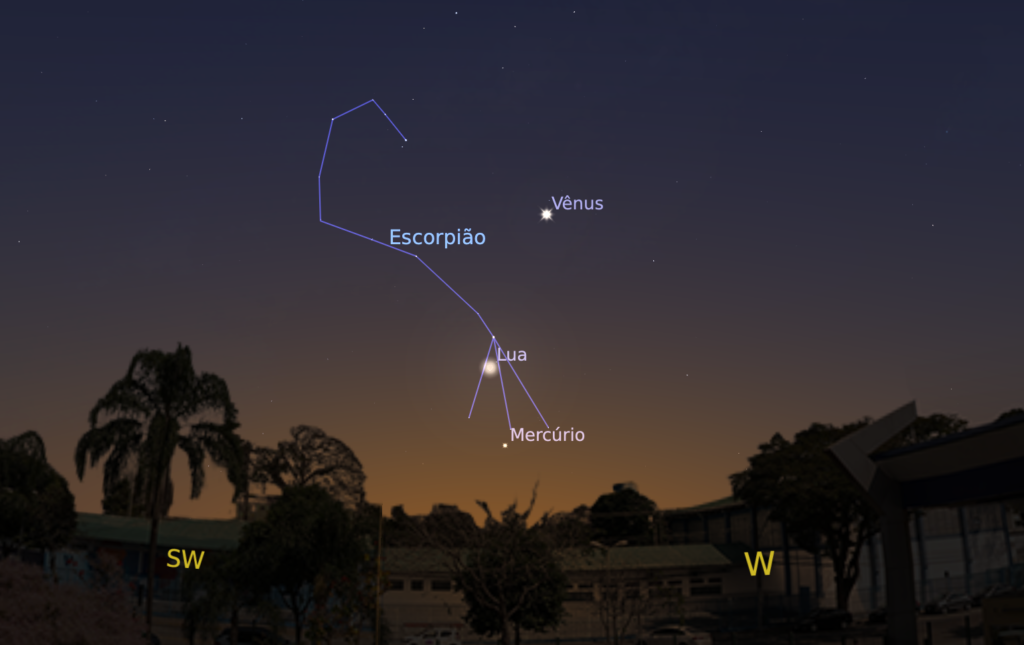
A simulação abaixo mostra a conjunção de Lua e Vênus no anoitecer do dia 3 de janeiro. Mas a cada dia, a Lua se desloca um pouco para leste e seguirá emparelhando com cada um dos planetas. Marte, Júpiter, Saturno e Vênus seguirão visíveis durante todo o mês de Janeiro, então se é alinhamento dos planetas que você quer, que tal observar a Lua em conjunção com cada um deles?

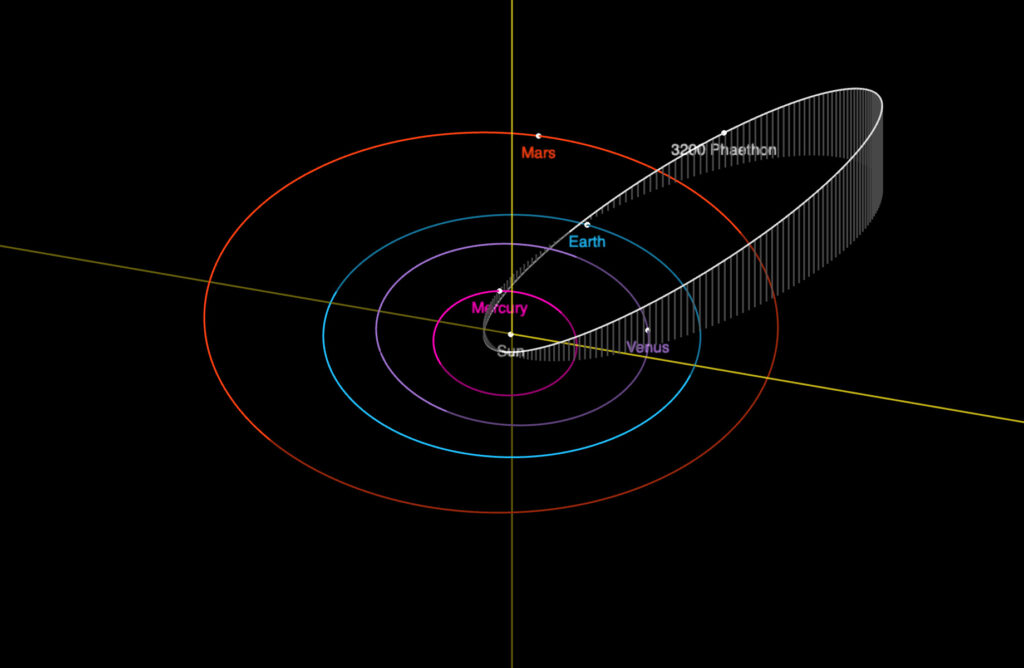
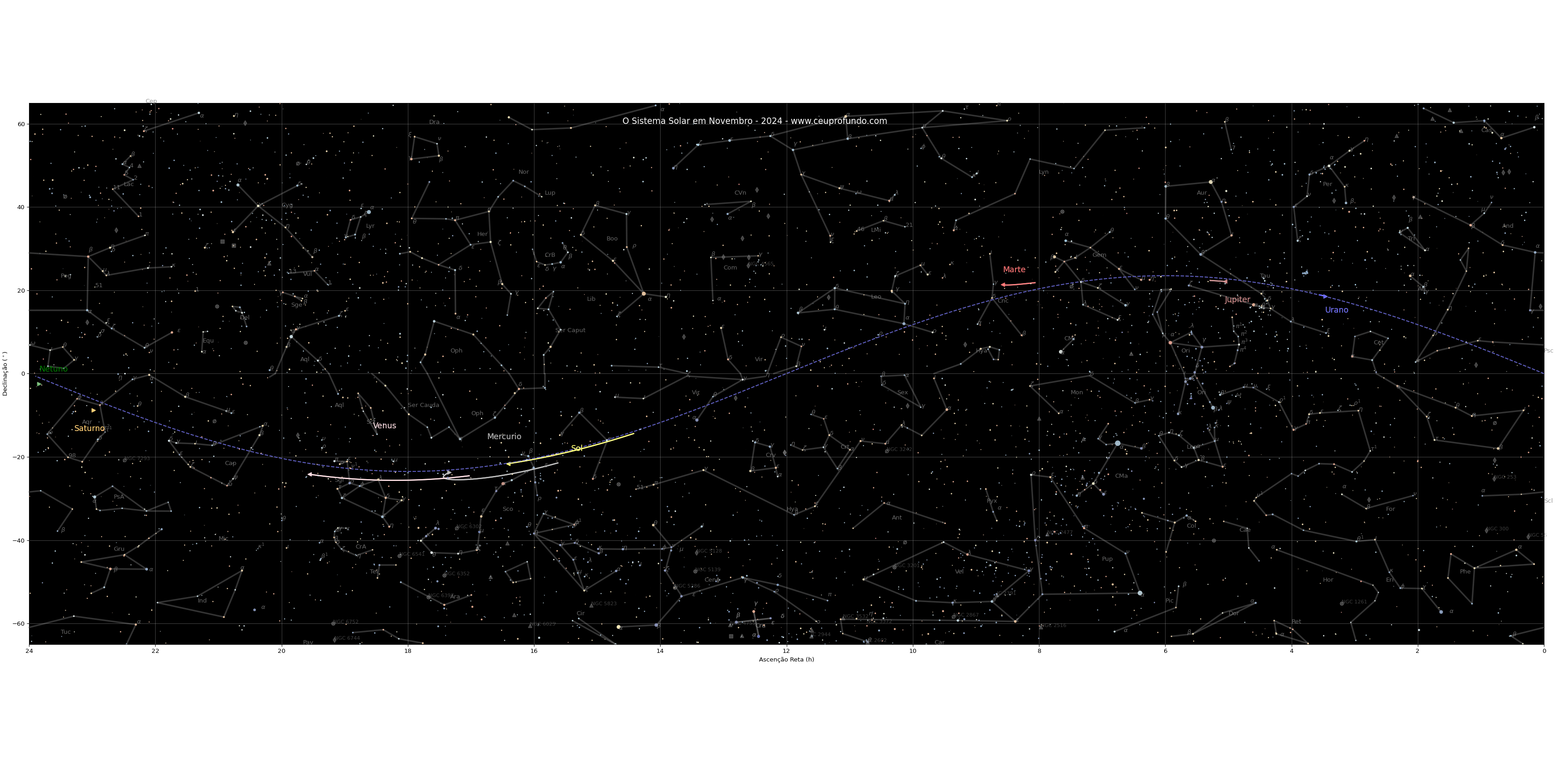
Utilizando o visualizador de órbitas do sitema Horizons do Laboratório de Propulsão a Jato da NASA, criamos essa visualização do sistema solar no dia 3 de janeiro, correspondendo a simulação acima. Podemos ver que os planetas orbitam aproximadamente no mesmo plano, mas que não estão alinhados.

E a moral da história?
A conclusão que podemos tirar não é exatamente uma novidade: tem muita gente falando bobagem e postando conteúdo sensacionalista sobre astronomia nas redes sociais para ganhar cliques (e dinheiro). Mas, felizmente, o Universo não precisa de sensacionalismo para ser um lugar sensacional!
Procure um lugar escuro, longe da poluição luminosa dos centros urbanos, e deleite-se com as belezas do céu. Mas nem precisa de telescópio pra isso. Um céu escuro pode revelar a olho nu dezenas de objetos de céu profundo, como nebulosas, aglomerados estelares e até algumas galáxias mais próximas.
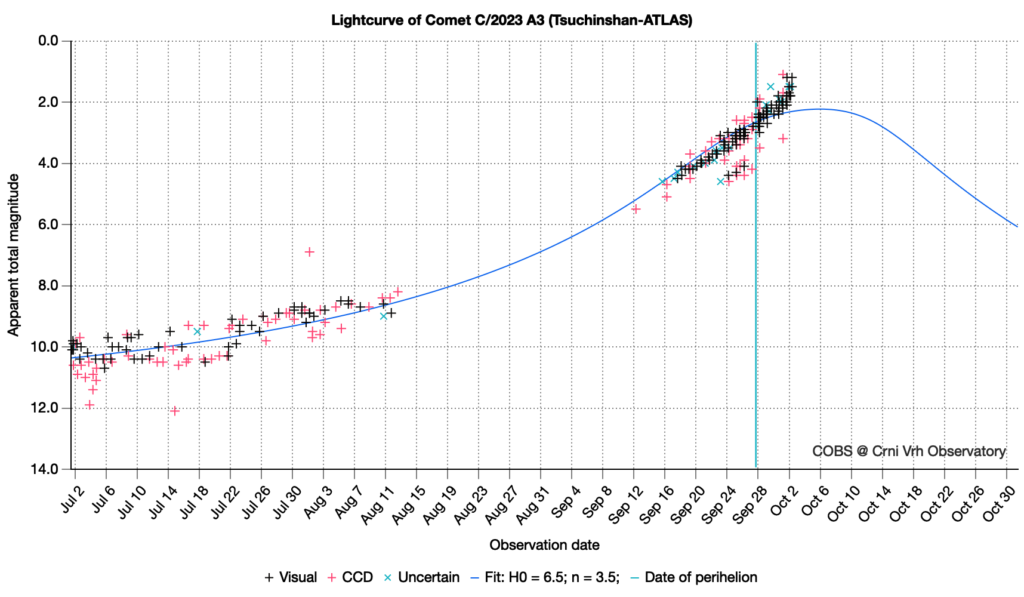
Com binóculos a experiência é ainda mais recompensadora, mergulhando em objetos mais extensos que sequer cabem inteiros no campo da ocular de um telescópio. Inclusive, binóculos são os instrumentos ideais para a observação de cometas (permitindo que vejamos uma grande extensão de sua cauda) e de conjunções planetárias, já que é incomum que os planetas fiquem próximos o suficiente para serem vistos simultaneamente através de um telescópio.